Computers are intuitively considered by many to be impeccably accurate with numbers. When we type any formula into a calculator or an Excel spreadsheet, we get perfect answers every time. However, if you were to type this line (>>> 0.1 + 0.2) into Python right now you will not get 0.3 like you might expect. Python will instead return this value (0.30000000000000004) and no, this is not a bug, this is the expected behaviour of the floating-point data type.
To explain this, lets first talk about Base 10, this is the decimal system we use in real life. In the positive direction from the decimal point, base ten is fundamentally separated into units, tens, hundreds, etc., and in the negative direction from the decimal point we have tenths, hundredths, thousandths, etc. Placing 0.1 into this system is simple, it is a single tenth.
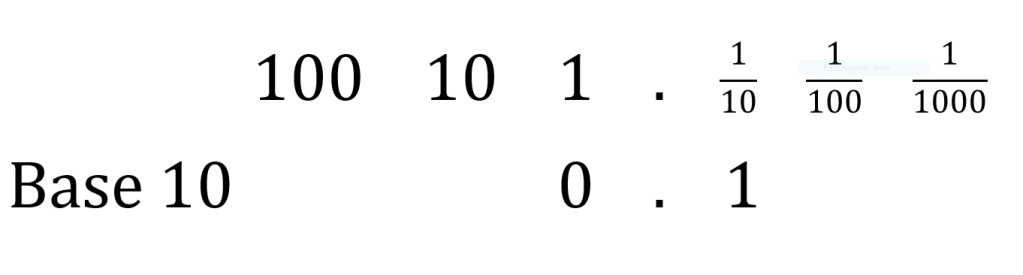
Computers on the other hand, at their purest level understand only two things, off and on, 0 and 1. As such, they can do not count in Base 10 because there are not ten varying states of off or on. Instead, they use Base 2, which separate numbers into ones, twos, fours, etc.; and on the other side of the decimal point separate in halves, quarters, eighths etc. So, to represent 0.1 in this system we 0.000110011…, where the 0011 continues to recur.

This is where the problem lies computer do not understand recurring numbers and python, being a 32-bit application only stores twenty-three significant digits. Now imagine you too, cannot understand recurring numbers and you are asked to add one third, plus one third, plus one third. Well, when doing this calculation with only twenty-three significant figures the answer does not equal one.
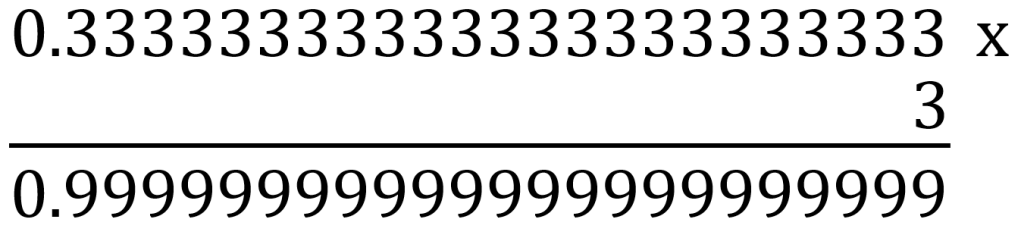
This is the exact problem with our original line of code (>>> 0.1 + 0.2), we were technically asking the computer:
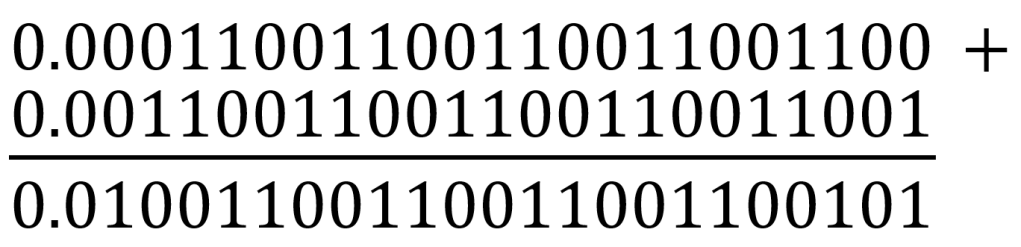
So, it returned its answer converted back to Base 10 (0.30000000000000004), it was not necessarily wrong it just was not precise.